��������ϵ
�� i��j ��ƽ�������������ص������� �����ƽ������һ����p �� ����Ψһһ��ʵ��x��y �� ʹ�� p = x i + y j . ����������ƽ����ѡ��һ��O��Ϊԭ�㣬 ��ƽ��������һ��P�� ��p = ����OP�� �ɴ˲����� ʵ���� x��y ���ǵ�P�����꣬ ��ԭ��O������ ƽ����i ��ֱ�߳�Ϊx�ᣬ ��ԭ��O������ ƽ����j ��ֱ�߳�Ϊy�ᣬ����������һ����������ϵ�� ע�����ڿ���ͨ�����Ա任��ֱ������ϵ��Ϊ�����ķ�������ϵ�� ����һ����Ԫ���Է��̴���ƽ���ϵ�һ��ֱ�ߣ� ��һ��ֱ��Ҳ����һ����Ԫ���Է�������ʾ��
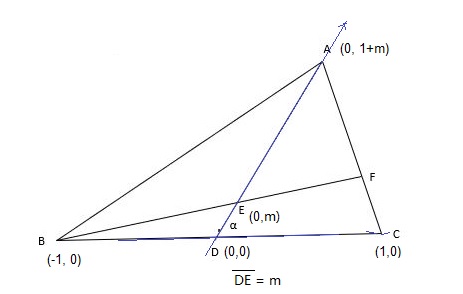
�ص�ƽ���ڵ��������� �� i��j ��������λ������ ���DΪԭ�㣬i ƽ���������εĵױߣ� ָ��\( C \)�� j ƽ����\( AD \)�� ָ��\( A\)�� ���� i ��j ֮��ļн�Ϊ\( \alpha��\) ���������ϵ�£� ƽ��������һ�� \( (X,Y) \)��ԭ������ƽ���� �������Ҷ����� ����\[ X^2 + Y^2 + 2XY \cos\alpha \].
�ټٶ� �����εױ߳���Ϊ2�� \( ED\)����Ϊ\( m\)�����Ǿ�����������ꡣ\( D��0��0��\)��Ȼ�ġ� ����
\( A(0, 1+m) \);
\( B( -1,0) \);
\( C( 1,0) \);
\( E( 0,m) \);
\( F \)��������ʲô��ע������ֱ��\( BE\)��\( AC\)�Ľ��㡣 ֻҪ���ֱ��\( BE\)��\( AC\)��Ӧ�Ķ�Ԫ���Է�����Ϳ����ˡ�
ֱ��\( BE\)�Ľؾ�ʽ����Ϊ\[ -x + \frac{y}{m} = 1;\] �� \[ y = m ( 1 + x), \] ���뵽 ֱ��\( AC\)�ķ���\[ x + \frac{y}{1+m} = 1, \] ��� \[ x = \frac{1}{2m + 1}, �� y = m + \frac{m}{2m + 1} .\]
\[ ��F(\frac{1}{2m + 1},m + \frac{m}{2m + 1} )\].
���棬 �ø�������꣬ ǰ���ᵽ�ľ���ƽ���Ĺ�ʽ�� �г�\( AF= FE \)�ķ��̣� ����� \( \alpha \) ��ֵ��
������ \( Ax�� Ay \)�ֱ��ʾ \(AF\)�� \(x�� y\)���ͶӰ��\(Ax= 1/(2m +1)\), \( Ay= m + m/(2m + 1)-1-m =-(m+1)/(2m +1)\).
ͬ����\( Ex�� Ey \)�ֱ��ʾ \(EF\)�� \(x�� y\)���ͶӰ��\( Ex= 1/(2m +1)\), \( Ey= m + m/(2m + 1)-m =m/(2m +1)\)��
��Ϊ\( AF ��EF\) ������ȣ� ��������ķ��̣�\[Ax^2 + Ay^2 + 2AxAy\cos\alpha = Ex^2 + Ey^2 + 2ExEy\cos\alpha ��\] ���� \( Ax = Ex = 1/(2m + 1)\), ��ȥ������ƽ������ \[ (Ay + Ey)(Ay - Ey) = 2Ax(Ey - Ay)\cos \alpha \]��\( Ay + Ey = - 1/(2m+1) = -Ax\), ���� \( 2\cos\alpha =1\), \( \alpha = \)60°.
���༭ʱ��: 2023-08-11 06:45:31


 [����]
[����]